enum class Type {
ID,
INTERFACE,
NUM,
WHITESPACE,
UNKNOWN,
}
data class TokenType(
val type: Type,
val pattern: Regex
)Lexical Analysis
1 Formal Languages
1.1 Building strings
1.1.1 Alphabet
We start with a finite collection of symbols, known as tokens, denoted by \(\Sigma\).
1.1.2 Strings
Given an alphabet \(\Sigma\), we can use symbols in \(\Sigma\) to build up strings of finite length.
All finite strings are denoted as \(\Sigma^*\).
1.1.3 Source code as strings
Consider a snippet of Java code.
interface Adder { int add(int a, int b); }
This is a string over some alphabet of lexemes.
1.1.4 Languages
A language is a subset of strings in \(\Sigma^*\).
\[ L \subseteq \Sigma^* \]
If some string \(s\in L\), then we say that \(s\) is valid with respect to the langauge \(L\).
1.2 Encoding of strings
1.2.1 Character based alphabet
Consider the alphabet:
\[ \Sigma_\mathrm{char} = \{a, b, c \dots, A, B, C, \dots \} \]
where each character is a lexeme.
All source code can be treated as strings over \(\Sigma_\mathrm{char}\).
1.2.2 Source code as character-based strings
interface Adder {
int add(int a, int b);
}Treating the code fragment as character based string:
interface → i-n-t-e-r-f-a-c-e- 47 characters = 47 symbols (including whitespaces).
1.2.3 Bit based alphabet
Consider the case of:
\[ \Sigma_\mathrm{bin} = \{0, 1\} \]
Each character is an integer (of 8 bits).
i → 105 → 01101001n → 110 → 01101110
1.2.4 Source code as binary strings
0110100101101110011101000110010101110010011001100110000
1011000110110010100100000010000010110010001100100011001
0101110010001000000111101100001010001000000010000001101
0010110111001110100001000000110000101100100011001000010
1000011010010110111001110100001000000110100100101100001
0000001101001011011100111010000100000011010100010100100
1110110000101001111101- \(s \in\Sigma_\mathrm{bin}^*\)
- 47 characters = 376 bits = 376 symbols in \(\Sigma_\mathrm{bin}\).
- Inefficient for algorithms to process long strings.
1.2.5 Changing alphabets
We can convert the encoding between different alphabets.
- \(h: \Sigma_\mathrm{bin}^* \to \Sigma_\mathrm{char}^*\)
- \(g: \Sigma_\mathrm{char}^* \to \Sigma_\mathrm{bin}^*\)
Example:
# Python
def h(s):
return [
chr(int(s[i:i+8], 2)) for i in range(0, len(s), 8)
]2 Tokenization
2.1 Designing better alphabet
- \(\Sigma\) is the set of symbols, we can tokens.
- There are categories of tokens in \(\Sigma\). They are also called token types.
- We can design token types to best encode strings of a language.
2.2 Alphabet for Java
'interface'is a token.'{', '}', '(', ')', ';', ','characters are kept as tokens.TYPEis a token type. It is used to represent all Java data types.IDis a token type. It is used to represent all possible Java identifiers (variable names, function names, …)
Let’s call this \(\Sigma_\mathrm{Java}\)
2.3 Encoding of Java programs
interface Adder {
int adder(int a, int b);
}becomes
'interface' ID '{'
TYPE ID '(' TYPE ID ',' TYPE ID ')' ';'
'}'- 14 tokens with the types indicated.
- But it is lossy as we cannot reconstruct the original string in \(\Sigma_\mathrm{char}^*\) from the lexemes.
- To make the encoding in \(\Sigma_\mathrm{Java}\) lossless, we define each token as (
token_type,lexeme). - A lexeme is the sub-string in the code that corresponds to the token.
Lexeme:
A substring in the source code that corresponds to a token of some type.
Token:
A unit of the source code that consists of:
- token type
- lexeme
2.4 Lexical analyzer
We can denote all possible tokens as \(\mathbf{Tok}\).
A lexical analyzer is a function:
\[ \mathrm{lex}: \Sigma^*_\mathrm{char} \to \mathbf{Tok}^* \]
3 General design of lexical analyzer
3.1 Defining token types
Each token type is defined as a regular expression.
Now, we can define the collection of token types.
val option = setOf(RegexOption.MULTILINE)
val tokenTypes = listOf(
TokenType(Type.ID, Regex("""\w[\w\d]*""", option)),
TokenType(Type.INTERFACE, Regex("interface", option)),
TokenType(Type.NUM, Regex("""\d+(\.\d+)?""", option)),
TokenType(Type.WHITESPACE, Regex("""\s+""", option)),
)3.2 Scanning the string
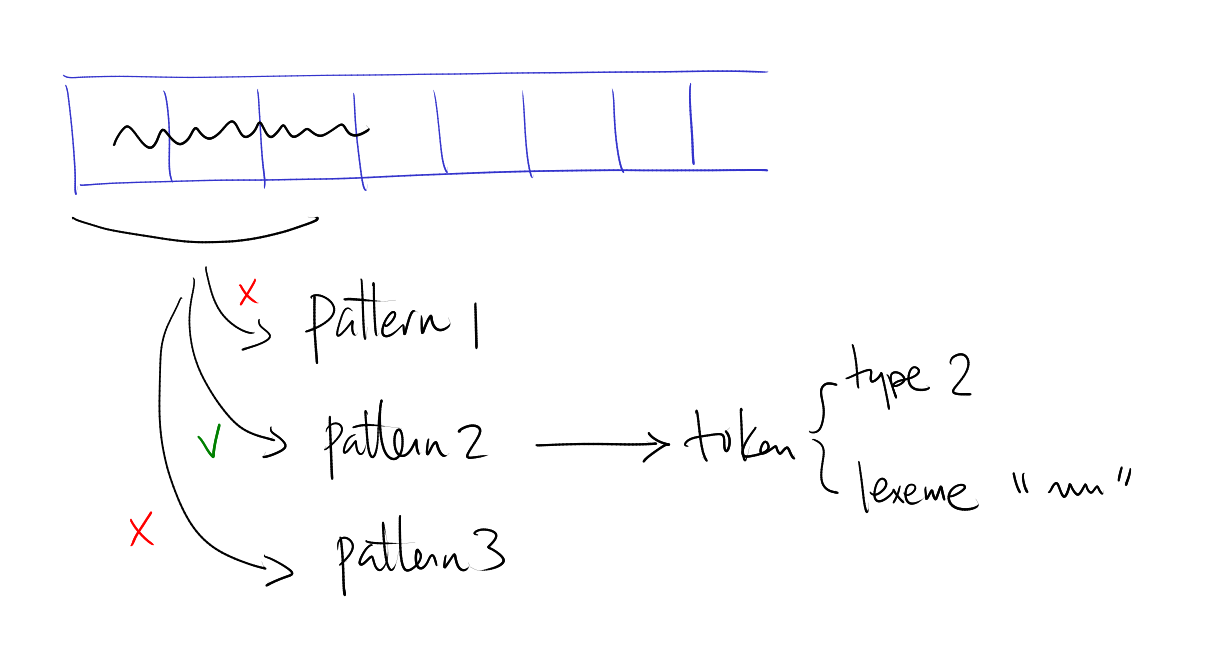
3.2.1 Left-right scan
- Start at the start of the string, and keep track of the
currentPosition: Int. - Try to match patterns at
currentPosition. Multiple patterns may apply. - Resolving ambiguity:
- Longest match rule: the longest possible match wins.
- Rule order: if two rules match the same length of characters, the rule that appeared first in the rule list wins.
data class Token(
val type: Type,
val lexeme: String,
val range: IntRange,
)interface Lexer {
val rules: List<TokenType>
fun next(s: String, p: Int): Token
}Let’s create an implementation of the Lexer interface.
val lexer = object: Lexer {
override val rules = tokenTypes
override fun next(s: String, p: Int): Token {
return rules.map {
val m = it.pattern.matchAt(s, p)
if(m != null)
Token(it.type, m.value, m.range)
else
Token(Type.UNKNOWN, s.substring(p, p+1), p..p)
}
.sortedBy { it.range.last }
.last()
}
}val source = "last_name = 123"
lexer.next(source, 0)Token(type=ID, lexeme=last_name, range=0..8)fun scan(s: String):Sequence<Token> = sequence {
var p = 0
while(p < s.length) {
val tok = lexer.next(s, p)
p = tok.range.last + 1
yield(tok)
}
}scan(source).forEach {
println(it)
}Token(type=ID, lexeme=last_name, range=0..8)
Token(type=WHITESPACE, lexeme= , range=9..9)
Token(type=UNKNOWN, lexeme==, range=10..10)
Token(type=WHITESPACE, lexeme= , range=11..11)
Token(type=NUM, lexeme=123, range=12..14)4 Summary
4.1 General lexical analyzer
- Lexical analyzer is a function that maps a character stream into a token stream.
- A lexical rule (aka lexer rule) is defined using regular expression.
- Ambiguity between lexical rules is resolved by:
- longest match wins
- if there are multiple longest matches, the first rule wins.